Unidad 15.
La representación de los datos
TEMA 14 ORIENTACIÓN EN EL PLANO
La representación de los datos
Ejercicios sobre tablas y gráficos estadísticos.
El jugador de Baloncesto: Técnicas de recogida de datos (encuesta, observación, medición)
La chica: Construcción de tablas de frecuencia
El hombre trajeado: Construcción de polígonos de frecuencias
El anciano con bastón y boina: Tablas de frecuencia relativa
La niña: Gráficos de sectores
El niño pequeño: Lectura e interpretación de gráficos estadísticos
Representación de datos: Gráficos. La Media
Lectura e interpretación de gráficos estadísticos
Es el ejercicio del niño pequeño del primer ejercicio
Tablas y Gráficos
En este ejercicio podrás hacer una tabla de intervalos de frecuencia y una vez realizado hacer un gráfico de barras.
TEMA 14 ORIENTACIÓN EN EL PLANO
Y EN EL ESPACIO
===LA ORIENTACIÓN (EL PLANO O EL MAPA)===
ieslasllamas
===COORDENADAS DE UN PUNTO EN EL PLANO===genmagic.org
===LA ESCALA===wikipedia.org
===EL PLANO===wikipedia.org
===COORDENADAS===
===NO PIERDAS EL NORTE===contenidos.proyectoagrega.es
===PLANO CARTESIANO===
juntadeandalucia/averroes
TEMA 13 LA MEDIDA DE SUPERFICIE
Unidades de Superficie.
| Kilómetro cuadrado | Km2 | 1.000.000 m2 |
| Hectómetro cuadrado | Hm2 | 10.000 m2 |
| Decámetro cuadrado | Dm2 | 100 m2 |
| metro cuadrado | m2 | 1 m2 |
| decímetro cuadrado | dm2 | 0,01 m2 |
| centímetro cuadrado | cm2 | 0,0001 m2 |
| milímetro cuadrado | mm2 | 0,000001 m2 |
MEDIDAS DE SUPERFICIE

Para medir superficies (áreas) se utilizan distintas unidades de medida. La más utilizada es el metro cuadrado (m2).
Un metro cuadrado es la superficie de un cuadrado cuyo lado mide un metro.

La superficie de un cuadrado es base por altura.
1 metro cuadrado = 1 metro X 1 metro = 1 m2
Se utiliza para medir la superficie de una habitación, la superficie de un jardín, la superficie de un apartamento...
1.- Unidades menores
Hay unidades de medidas menores que se utilizan para medir áreas más pequeñas (la superficie de una loza, de un folio, de la pantalla digital de un teléfono móvil, …).
Decímetro cuadrado (dm2). Es la superficie de un cuadrado cuyo lado mide un decímetro.
Centímetro cuadrado (cm2). Es la superficie de un cuadrado cuyo lado mide un centímetro.
Milímetro cuadrado (mm2). Es la superficie de un cuadrado cuyo lado mide un milímetro.
La relación con el metro es:
1 m2 = 100 dm2.
La relación de las unidades de superficie va de 100 en 100 (en lugar de 10 en 10).
1 metro cuadrado = 1 metro x 1 metro
1 metro = 10 decímetros
1 metro cuadrado = 10 decímetros x 10 decímetros = 100 decímetros cuadrados
1 m2 = 10.000 cm2
1 metro = 100 centímetros
1 metro cuadrado = 100 centímetros x 100 centímetros = 10.000 centímetros cuadrados.
1 m2 = 1.000.000 mm2
1 metro = 1.000 milímetros
1 metro cuadrado = 1.000 milímetros x 1.000 milímetros = 1.000.000 milímetros cuadrados.
La relación entre ellas es:
1 dm2 = 100 cm2
1 dm2 = 10.000 mm2
1 cm2 = 100 mm2
2.- Unidades mayores
También hay unidades de medidas mayores que el metro cuadrado que se utilizan para medir grandes superficies: la superficie de una provicina, de una finca, de un lago...
Kilómetro cuadrado (km2). Es la superficie de un cuadrado cuyo lado mide un kilómetro.
Hectómetro cuadrado (hm2). Es la superficie de un cuadrado cuyo lado mide un hectómetro.
Decámetro cuadrado (dam2). Es la superficie de un cuadrado cuyo lado mide un decámetro.
La relación con el metro es:
1 km2 = 1.000.000 m2
1 hm2 = 10.000 m2
1 dam2 = 100 m2
La relación entre ellas también va de 100 en 100:
1 km2 = 100 hm2
1 km2 = 10.000 dam2
1 hm2 = 100 dam2

3.- ¿Cómo pasar de unidades mayores a unidades menores?
Para pasar de unidades mayores a unidades menores hay que multiplicar por 100 por cada nivel que descendamos:

Por ejemplo:
Para pasar de km2 a dam2 hay que bajar 2 niveles por lo que tenemos que multiplicar: x 100 x 100 = x 10.000Para pasar de hm2 a dm2 hay que bajar 3 niveles por lo que tenemos que multiplicar: x 100 x 100 x 100 = x 1.000.000
Veamos algunos ejemplos numéricos:
¿Cuantos m2 son 3 km2? 3 x 1.000.000 = 3.000.000 m2
¿Cuantos mm2 son 5 dm2? 5 x 10.000 = 50.000 mm2
¿Cuantos cm2 son 7 dam2? 7 x 1.000.000 = 7.000.000 cm2
4.- ¿Cómo pasar de unidades menores a unidades mayores?
Para pasar de unidades menores a unidades mayores hay que dividir por 100 por cada nivel que subamos:

Por ejemplo:
Para pasar de m2 a hm2 hay que subir 2 niveles por lo que tenemos que dividir : 100 : 100 = : 10.000Para pasar de cm2 a dam2 hay que subir 3 niveles por lo que tenemos que dividir : 100 : 100 : 100 = : 1.000.000
Veamos algunos ejemplos numéricos:
¿Cuantos m2 son 60.000 cm2? 60.000 : 10.000 = 6 m2
¿Cuantos km2 son 8.000.000 m2? 8.000.000 : 1.000.000 = 8 km2
¿Cuantos dm2 son 75.000 mm2? 75.000 : 10.000 = 7,5 dm2
Área de PARALELOGRAMOS
El área de un paralelogramo cualquiera es el producto de la base por la altura:
A = base · altura = b · h
Los paralelogramos son los cuadrados, rectángulos, rombos y romboides.
Área del cuadrado
Área del rectángulo
Área del rombo
Observamos que el rombo, de diagonales D y d, ocupa la mitad de superficie que un rectángulo de lados D y d.
Área del romboide
El romboide también es un paralelogramo; por tanto, su área es el producto de la base por la altura.
A = b · h
Área de TRIÁNGULOS
El área de un triángulo es igual a base por altura partido por 2.
La altura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación).
Ejemplo
Hallar el área del siguiente triángulo:
Área de un triángulo equilátero
Ejemplo
Calcular el área de un triángulo equilátero de 10 cm de lado.
Área de un triángulo rectángulo
El área de un triángulo rectángulo es igual al producto de los catetos partido por 2.

Ejemplo
Calcular el área del triángulo rectángulo cuyos catetos miden 3 y 4 cm.

Ahora pincha sobre cualquiera de esta figuras y descubrirás su ÁREA
La superficie.Juegos. Pincha aquí
TEMA 12 LAS FIGURAS PLANAS
| Definiciones -> E -> Eje de simetría |
Eje de simetría | |
 | Una línea que atraviesa una figura de tal manera que cada lado es el espejo del otro. Si dobláramos la figura en la mitad a lo largo del Eje de Simetría, tendríamos que las dos mitades son iguales, quedarían parejas. |

figuras iguales


y figuras diferentes
FIGURAS PLANAS

Un polígono está formado por una línea poligonal cerrada y la superficie interior.
Todos sus lados tienen que ser líneas rectas.

Veamos ahora 2 figuras que no son polígonos:
Porque son líneas abiertas
O porque alguno de sus lados no es una línea recta
 ..................
..................
En un polígono se pueden distinguir:
- Lados
- Vértices
- Ángulos
- Diagonales (líneas rectas que unen dos vértices no consecutivos)

La suma de la longitud de sus lados se denomina perímetro.
La superficie interior de un polígono se llama área.

Según el número de lados, los polígonos se clasifican en:
Triángulo: 3 lados
Cuadrilátero: 4 lados
Pentágono: 5 lados
Hexágono: 6 lados
Heptágono: 7 lados
Octógono: 8 lados
Eneágono: 9 lados
Decágono: 10 lados
Cuando todos los lados de un polígono son iguales se denomina polígono regular. También sus ángulos son iguales.
 |  | |
.
| ||
Triángulo regular
|
Cuadrilátero regular
| |
.
| ||
 |  | |
.
| ||
Pentágono regular
|
Hexágono regular
| |
 |  | |
Heptágono regular
|
Octógono regular
|
Como todos sus lados son iguales, su perímetro se puede calcular multiplicando la longitud de un lado por el número de lados:

Por ejemplo, el lado de este hexágono regular mide 5 cm, por lo que su perímetro será:
Perímetro = 5 x 6 (nº de lados) = 30 cm
Polígonos cóncavos y convexos
Un polígono que tiene todos sus ángulos menores de 180° se denomina polígono convexo. Si alguno de sus ángulos es mayor de 180°, se llama polígono cóncavo.
1.- El triángulo
Los triángulos se pueden clasificar según sus lados:
Triángulo equilátero: todos sus lados son iguales
Triángulo isósceles: tiene 2 lados iguales
Triángulo escaleno: todos sus lados son diferentes
 |  |  | ||
.
| ||||
Triángulo equilátero
|
Triángulo isósceles
|
Triángulo escaleno
|
Los triángulos también se pueden clasificar según sus ángulos:
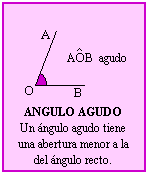
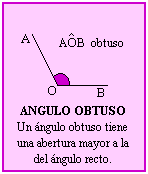
Triángulo rectángulo: un ángulo recto y dos agudos
Triángulo acutángulo: todos sus ángulos son agudos
Triángulo obtusángulo: uno de sus ángulos es obtuso
 |  |  | ||
.
| ||||
Triángulo rectángulo
|
Triángulo acutángulo
|
Triángulo obtusángulo
|
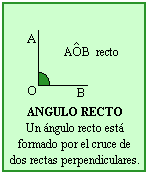
En el triángulo rectángulo podemos distinguir:
Los dos lados que forman el ángulo recto se denominan catetos
El lado opuesto al ángulo recto se denomina hipotenusa

2.- El cuadrilátero

Se pueden clasificar en:
Paralelogramos: sus lados son paralelos dos a dos.

No paralelogramos: aquellos que no cumplen esta condición.

Los cuadriláteros paralelogramos se pueden clasificar en:
Cuadrado: 4 lados iguales y 4 ángulos rectos
Rectángulo: 4 lados iguales dos a dos y 4 ángulos rectos
Rombo: 4 lados iguales, y 2 ángulos agudos y 2 ángulos obtusos
Romboide: 4 lados iguales dos a dos , y 2 ángulos agudos y 2 ángulos obtusos
 |  | |
.
| ||
Cuadrado
|
Rectángulo
| |
.
| ||
 |  | |
.
| ||
Rombo
|
Romboide
|
Los cuadriláteros no paralelogramos pueden ser:
Trapecio: Tiene 2 lados paralelos y los otros 2 no.
Trapezoide: Ninguno de sus lados es paralelo
 |  | |
.
| ||
Trapecio
|
Trapezoide
|
El trapecio se puede clasificar en:
Trapecio rectángulo: 2 de sus ángulos son rectos

Trapecio isósceles: tiene 2 lados opuestos iguales y sus ángulos son iguales 2 a 2.

Trapecio escaleno: todos sus lados son diferentes


3.- La circunferencia y el círculo
La circunferencia es una curva cerrada en la que todos sus puntos están a la misma distancia del centro.
El interior de la circunferencia y la propia circunferencia forman un círculo.

Podemos distinguir los siguientes elementos:
Diámtero: Es la línea recta que va de lado a lado de la circunferencia pasando por el centro del círculo.

Radio: Es la línea recta que va desde el centro del círculo hasta la circunferencia.

Cuerda: Es la línea recta que va de lado a lado de la circunferencia sin pasar por el centro del círculo.

La mitad de un círculo se llema semicírculo:

Una sección del círculo limitada por 2 radios y la circunferencia se llama sector circular.

Una sección del círculo limitada por una cuerda y la circunferencia se llama segmento circular.

4.- Figura simétrica
Una figura simétrica es aquella en la que sus dos mitades son iguales. La línea que divide la figura en dos partes se denomina eje de simetría.
Figura simétrica

Figura no simétrica

El número Pi es aquel que multiplicando el diámetro por él, nos da la longitud de una circunferencia
Demostración práctica del número PI
TEMA 11 LOS ÁNGULOS
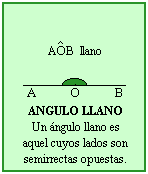
ÁNGULOS
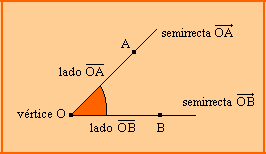
Ángulo es la figura formada por 2 semirrectas que parten de un mismo punto. Las semirrectas se llaman lados y el punto común vértice.
SISTEMAS DE MEDICIÓN DE ÁNGULOS
Sistema sexagesimal
Se divide la circunferencia en 360 partes iguales y cada una de estas partes constituye un grado sexagesimal.
|
|
Los ángulos según su posición pueden ser:
| ||
 |  |  |
CONSECUTIVOS
|
ADYACENTES
|
OPUESTOS POR EL VÉRTICE
|

COMO MEDIR UN ÁNGULO
ÁNGULOS COMPLEMENTARIOS Y SUPLEMENTARIOS
TEMA 10 LA MEDIDA DEL TIEMPO
EL TIEMPO HISTÓRICO
LAS HORAS, LOS MINUTOS, LOS SEGUNDOS.
EXPRESIONES COMPLEJAS E INCOMPLEJAS
OPERACIONES CON UNIDADES DE MEDIDA DE TIEMPO
LAS SIGUIENTES IMÁGENES SON FRUTO DEL TRABAJO DE DON PACO.
ES UN PERFECTO RESUMEN DEL TEMA

 ENLACE: TRABAJAMOS CON EL TIEMPO
ENLACE: TRABAJAMOS CON EL TIEMPOENLACE: TRABAJAMOS CON EL TIEMPO 2
TEMA 9 LA CAPACIDAD Y EL PESO
UNIDADES DE CAPACIDAD Y PESO
Resulta primordial conocer las diferentes unidades de medida (como en el tema anterior) tanto de capacidad como de peso.
UNIDADES MEDIDA DE CAPACIDAD
| ||||||
MULTIPLOS
|
UNIDAD
PRINCIPAL
|
SUBMULTIPLOS
| ||||
Kl
|
hl
|
dal
|
l
|
dl
|
cl
|
ml
|
Kilolitro
|
Hectolitro
|
Decalitro
|
Litro
|
Decilitro
|
Centilitro
|
mililitro
|
UNIDADES MEDIDA DE PESO
| ||||||
MULTIPLOS
|
UNIDAD
PRINCIPAL
|
SUBMULTIPLOS
| ||||
Kg
|
hg
|
dag
|
g
|
dg
|
cg
|
mg
|
Kilogramo
|
Hecto
|
Deca
|
Gramo
|
Deci
|
Centigramo
|
miligramo
|
CAPACIDAD
En la siguiente tabla de posición se muestran el nombre, la abreviatura y el valor de los múltiplos (kl,hl,dal) y submúltiplos (dl, cl, ml) más usuales del litro. En algunos libros el hectolitro se abrevia como Hl y el decalitro como Dl.
| kilolitro | hectolitro | decalitro | litro | decilitro | centilitro | mililitro |
| kl | hl | dal | l | dl | cl | ml |
| 1.000 l | 100 l | 10 l | 1 l | 0,1 l | 0,01 l | 0,001 l |
Como puede observarse en la tabla de posición, el valor de cada unidad es 10 veces mayor que el valor de la unidad situada a su derecha. Es decir:
1 kl = 10 hl = 100 dal = 1.000 l = 10.000 dl = 100.000 cl = 1.000.000 ml.
Para convertir una unidad determinada en otra pedida, situada a su derecha(menor), tenemos que multiplicarla por la unidad seguida de tantos ceros como posiciones hay, en la tabla, entre la unidad determinada y la pedida.
Recuerda que multiplicar por la unidad seguida de ceros equivale a "correr la comade los decimales" hacia la derecha tantos lugares como ceros acompañan a la unidad.
Ejemplo: Convertir 7 hl en dl.
Como desde hl a dl hay 3 posiciones, hacia la derecha, tendremos que multiplicarpor 1000. Por lo tanto, 7 hl = 7 x 1.000 = 7.000 dl.
Lo que equivale a correr la coma 3 lugares a la derecha: 7,0000 X 1.000 = 7.000,0
(Los ceros a la derecha de la coma de decimales no tienen valor y podemos poner los que necesitemos)
Lo que equivale a correr la coma 3 lugares a la derecha: 7,0000 X 1.000 = 7.000,0
(Los ceros a la derecha de la coma de decimales no tienen valor y podemos poner los que necesitemos)
Para convertir una unidad determinada en otra pedida, situada a su izquierda(mayor), tenemos que dividirla por la unidad seguida de tantos ceros como posiciones hay, en la tabla, entre la unidad determinada y la pedida.
Recuerda que dividir por la unidad seguida de ceros equivale a "correr la coma de los decimales" hacia la izquierda tantos lugares como ceros acompañan a la unidad.
PESO
En la siguiente tabla de posición se muestran el nombre, la abreviatura y el valor de los múltiplos (kg,hg,dag) y submúltiplos (dg, cg, mg) más usuales delgramo. En algunos libros de Matemáticas el hectogramo se abrevia como Hg y el decagramo como Dg.
| kilogramo | hectogramo | decagramo | gramo | decigramo | centigramo | miligramo |
| kg | hg | dag | g | dg | cg | mg |
| 1.000 g | 100 g | 10 g | 1 g | 0,1 g | 0,01 g | 0,001 g |
Como puede observarse en la tabla de posición, el valor de cada unidad es 10 veces mayor que el valor de la unidad situada a su derecha. Es decir:
1 kg = 10 hg = 100 dag = 1.000 g = 10.000 dg = 100.000 cg = 1.000.000 mg.
Para convertir una unidad determinada en otra pedida, situada a su derecha(menor), tenemos que multiplicarla por la unidad seguida de tantos ceros como posiciones hay, en la tabla, entre la unidad determinada y la pedida.
Recuerda que multiplicar por la unidad seguida de ceros equivale a "correr la coma de los decimales" hacia la derecha tantos lugares como ceros acompañan a la unidad.
Ejemplo: Convertir 8 dag en dg.
Como desde dag a dg hay 2 posiciones, hacia la derecha, tendremos que multiplicarpor 100. Por lo tanto, 8 dag = 8 x 100 = 800 dg.
Lo que equivale a correr la coma 2 lugares a la derecha: 8,000 X 100 = 800,0
(Los ceros a la derecha de la coma de decimales no tienen valor y podemos poner los que necesitemos)
Lo que equivale a correr la coma 2 lugares a la derecha: 8,000 X 100 = 800,0
(Los ceros a la derecha de la coma de decimales no tienen valor y podemos poner los que necesitemos)
Para convertir una unidad determinada en otra pedida, situada a su izquierda(mayor), tenemos que dividirla por la unidad seguida de tantos ceros como posiciones hay, en la tabla, entre la unidad determinada y la pedida.
Recuerda que dividir por la unidad seguida de ceros equivale a "correr la coma de los decimales" hacia la izquierda tantos lugares como ceros acompañan a la unidad.
Aprende y juega con la medidas de capacidad
Aprende y juega con la medida de peso
TRABAJAMOS LAS UNIDADES
PASAR DE FORMA INCOMPLEJA A COMPLEJA
Pasar de una medida expresada en forma compleja a incompleja
¿Cómo pasamos una medida expresada en forma compleja a incompleja?
- Para pasar de forma incompleja a compleja. Usamos el cuadro de unidades, colocando cada cifra en su lugar adecuado.
Observamos que la cifra que indica los metros es 2, justo la anterior a la coma.
- Para pasar de forma compleja a incompleja. Podemos utilizar el cuadro de unidades, como en el caso anterior, o pasar todas las unidades a la unidad indicada.Así, para pasar 4 hm 5 m 7 cm a milímetros:4 hm 5 m 7 cm = 400.000 mm + 5.000 mm + 70 mm = 405.070 mm
TEMA 8 LA MEDIDA DE LONGITUD
Curiosidades:
Antes de la adopción del Sistema Métrico Decimal cada provincia de un país usaba medidas distintas. Por ejemplo, la vara era una unidad de longitud muy usual pero tenía distintos valores en cada zona.
En 1795 tratando de hacer un sistema de medidas lógico y sencillo de aprender, un comité de científicos franceses creó el Sistema Métrico Decimal, que fue adoptado poco a poco por la mayor parte de los países. El nuevo estándar de longitud se relacionaba con las dimensiones de la tierra en lugar de a las dimensiones de un hombre.
En España se declaró oficial en 1849
Las unidades del sistema fueron definidas de modo que se relacionaran unas con otras en unidades de diez, es decir, para que encajaran en el sistema decimal de contar. Además se hizo un intento para establecer una relación simple entre las unidades de longitud, volumen y masa.
La unidad básica de longitud es el metro (39.37 pulgadas EE.UU)
A mediados del siglo pasado estaba muy claro que el sistema era insuficiente para las nuevas medidas que se necesitaban en aquellos momentos, por ejemplo, había distancias mucho más pequeñas y más grandes de las previstas inicialmente, por eso en 1960 se reunió un comité internacional para actualizarlo, lo hicieron, y al nuevo sistema resultante le llamaron Sistema Internacional de Medidas (SI). Desde entonces funciona un comité que añade nuevas unidades cuando es necesario; por ejemplo en 1991 se añadieron zetta (1021), zepto (10-21), yotta (1024) y yocto (10-24).
LAS UNIDADES DE MEDIDA DE LONGITUD
MULTIPLOS
|
UNIDAD
PRINCIPAL
|
SUBMULTIPLOS
| ||||
Km
|
hm
|
dam
|
m
|
dm
|
cm
|
mm
|


ENLACES PARA TRABAJAR Y COMPRENDER
Actividades propuestas por la editorial ANAYA
TEMA 6 Y 7 LAS FRACCIONES
http://cp.claracampoamor.fuenlabrada.educa.madrid.org/juegosporareas-matematicas.htm#FRACCIONES
























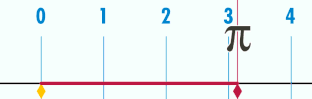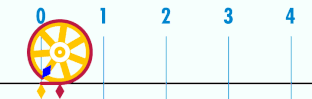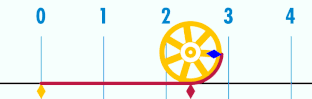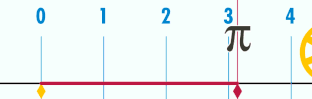
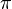 es la relación entre la longitud de una
es la relación entre la longitud de una